Cycloconverter
交流電力の周波数変換をする方式にサイクロコンバータがある。動作原理がわからなかったが数式を解くことで理解が進むか試してみる。
Switch の定義
角速度ωsで進行する矩形波を定義する。スイッチのイメージ。
S(\theta) =
\begin{cases}
1 &\text{if } 0 < \theta \leqq \pi \\
-1 &\text{if } \pi < \theta \leqq 2\pi
\end{cases}
\qquad\theta = \omega_s tコンバータの出力電圧
角速度ωcで進行する搬送波を定義してS(θ)で変調する。
v = S(\theta)\cdot V_m\cos\omega_c tS(θ) のフーリエ級数展開
ここでS(θ)のフーリエ級数展開を整理しておく。
\begin{aligned}
S(\theta) & = \frac{a_0}{2} + \sum_{n=1}^{\infin}(a_n\cos n\theta + b_n\sin n\theta) \\
a_0 & = \frac{1}{\pi}\int_{0}^{2\pi}S(\theta)\,d\theta \\
& = \frac{1}{\pi}\int_{0}^{\pi}(1)\,d\theta + \frac{1}{\pi}\int_{\pi}^{2\pi}(-1)\,d\theta \\
& = \frac{1}{\pi}\Big[\theta\Big]_{0}^{\pi} + \frac{1}{\pi}\Big[-\theta\Big]_{\pi}^{2\pi} \\
& = 0 \\
a_n & = \frac{1}{\pi}\int_{0}^{2\pi} S(\theta)\cos n\theta\,d\theta \\
& = \frac{1}{\pi}\int_{0}^{\pi} \cos n\theta\,d\theta + \frac{1}{\pi}\int_{\pi}^{2\pi} (-\cos n\theta)\,d\theta \\
& = \frac{1}{\pi}\left[\frac{1}{n} \sin n\theta\right]_{0}^{\pi} + \frac{1}{\pi}\left[-\frac{1}{n} \sin n\theta\right]_{\pi}^{2\pi} \\
& = 0 \\
b_n & = \frac{1}{\pi}\int_{0}^{2\pi} S(\theta)\sin n\theta\,d\theta \\
& = \frac{1}{\pi}\int_{0}^{\pi} \sin n\theta\,d\theta + \frac{1}{\pi}\int_{\pi}^{2\pi} (-\sin n\theta)\,d\theta \\
& = \frac{1}{\pi}\left[-\frac{1}{n} \cos n\theta\right]_{0}^{\pi} + \frac{1}{\pi}\left[\frac{1}{n} \cos n\theta\right]_{\pi}^{2\pi} \\
& = \frac{2}{\pi}(1 - \cos n\pi) \\
S(\theta) & = \sum_{n=1}^{\infin} \frac{2}{n\pi}(1 - \cos n\pi) \sin n\theta \\
& = \frac{4}{\pi} \left( \sin\omega_s t +\frac{1}{3}\sin 3\omega_s t +\frac{1}{5}\sin 5\omega_s t +\frac{1}{7}\sin 7\omega_s t + \cdots \right) \\
\end{aligned}この式から基本次数とその奇数倍の周波数成分からなるスペクトルを持つことがわかる。矩形波ですものね。
サイクロコンバータの出力電圧
サイクロコンバータの変調式へフーリエ級数展開式を代入してみる。
\begin{aligned}
v & = S(\theta)\cdot V_m\cos\omega_c t \\
& = \frac{4}{\pi} \left( \sin\omega_s t +\frac{1}{3}\sin 3\omega_s t +\frac{1}{5}\sin 5\omega_s t +\frac{1}{7}\sin 7\omega_s t + \cdots \right) V_m \cos\omega_c t \\
& = \frac{4V_m}{\pi} \Big(
\sin\omega_s t \cos\omega_c t
+ \frac{1}{3}\sin 3\omega_s t \cos\omega_c t \\
& \qquad + \frac{1}{5}\sin 5\omega_s t \cos\omega_c t
+ \frac{1}{7}\sin 7\omega_s t \cos\omega_c t
+ \cdots \Big) \\
& = \frac{2V_m}{\pi} \Big\{
\sin(\omega_s + \omega_c)t + \sin(\omega_s - \omega_c)t \\
& \qquad + \frac{1}{3} \sin(3\omega_s + \omega_c)t + \frac{1}{3} \sin(3\omega_s - \omega_c)t \\
& \qquad + \frac{1}{5} \sin(5\omega_s + \omega_c)t + \frac{1}{5} \sin(5\omega_s - \omega_c)t \\
& \qquad + \frac{1}{7} \sin(7\omega_s + \omega_c)t + \frac{1}{7} \sin(7\omega_s - \omega_c)t + \cdots \Big\}
\end{aligned}角速度
\text{Angular Velocity: } \omega_f = \omega_s - \omega_cSimulation
jupyter notebook で計算してみる。
import numpy as np
import matplotlib.pyplot as plt
fs = 44.0 # [Hz]
fc = 50.0 # [Hz]
Os = 2.0 * np.pi * fs # [rad/s]
Oc = 2.0 * np.pi * fc # [rad/s]
t = np.linspace(0, 1.0, 10000) # [s]
v = (2.0/np.pi)*((np.sin((Os+Oc)*t)+np.sin((Os-Oc)*t)) + (1.0/3.0)*(np.sin((3.0*Os+Oc)*t)+np.sin((3.0*Os-Oc)*t))
+ (1.0/5.0)*(np.sin((5.0*Os+Oc)*t)+np.sin((5.0*Os-Oc)*t)) + (1.0/7.0)*(np.sin((7.0*Os+Oc)*t)+np.sin((7.0*Os-Oc)*t)))
plt.figure(figsize=(10,4))
plt.plot(t, v)
vlpf = np.array(v)
vlpf[0] = v[0]
for i in range(np.size(v,0)-1):
vlpf[i + 1] = (1.0 - 0.998) * v[i+1] + 0.998 * vlpf[i]
plt.plot(t, vlpf)
plt.show()計算結果
青色が出力波形で、橙色はLPFをかけた波形である。50Hzの交流を44Hzでスイッチングすることでおおよそ6Hzの交流が現れた。
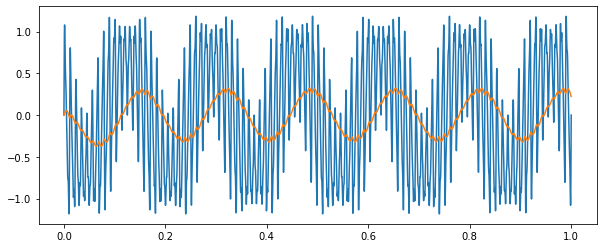
波形を重畳して計算
搬送波と変調波を直接積算して波形を描画してみよう。
jupyter notebook で計算してみる。
import numpy as np
import matplotlib.pyplot as plt
fs = 44.0 # [Hz]
fc = 50.0 # [Hz]
Os = 2.0 * np.pi * fs # [rad/s]
Oc = 2.0 * np.pi * fc # [rad/s]
t = np.linspace(0, 1.0, 10000) # [s]
vc = np.sin(Oc * t)
vs = np.sign(np.sin(Os * t))
vo = vc * vs
plt.figure(figsize=(10,4))
plt.plot(t, vo)
volpf = np.array(vo)
volpf[0] = vo[0]
for i in range(np.size(vo,0)-1):
volpf[i + 1] = (1.0 - 0.998) * vo[i+1] + 0.998 * volpf[i]
plt.plot(t, volpf)
plt.show()計算結果
青色が出力波形で、橙色はLPFをかけた波形である。50Hzの交流を44Hzでスイッチングすることでおおよそ6Hzの交流が現れた。
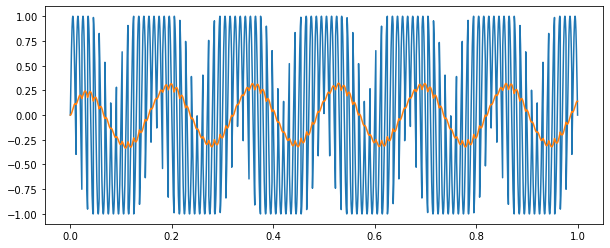
実際に励磁すると振動が大きくなりそうだが...どうなんでしょう。