自家用車の燃費推移の周波数分析

一体何を言っているのだ。と思われそうだが、ガソリンの給油のたびに燃費を計算して記録していたので、そのデータをフーリエ変換したくなったのだ。

諸元

対象車	トヨタ　アクア　2013
集計期間	2013 〜 2022
燃費計算	満タン法
備考	通勤に使用　毎日往復50km

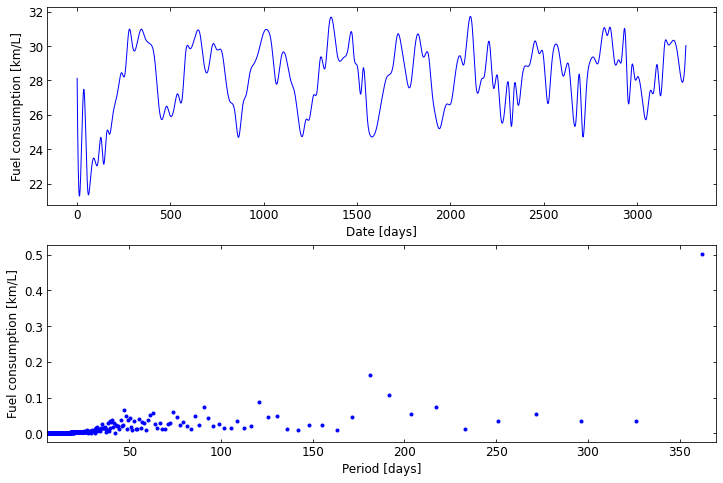
結果

上のグラフは横軸は経過日数[days]、縦軸が燃費[km/L]で、燃費の推移である。
下のグラフは横軸は周期[days]、縦軸が周期に対する燃費振れ成分[km/L]である。365日(1年)と180日(半年)付近にピークがある。おそらく夏はエアコン、冬は暖房の使用で燃費が落ちるのだろう。

計算方法

燃費データをcsvフォーマットで作成する。1列目に経過日数、2列目を燃費とする。燃費はガソリンを満タン補給する度に走行距離と給油量から算出した。

燃費データcsvファイル例

[days],[km/L]
18,28.122
34,21.676
54,27.475
73,21.922
89,22.234
107,23.484
~~~~~~~~
3221,30.254
3238,29.365
3257,27.977
3280,30.023

jupyter で作成し動作確認したソースコード

#!/usr/bin/env python
# coding: utf-8

# In[1]:

import numpy as np
import matplotlib.pyplot as plt
from scipy import interpolate
from scipy import fftpack

# In[2]:

# csvファイルの読み込み
filename = 'fuelconsumption.csv'
data = np.loadtxt(filename,delimiter=",",skiprows=1, dtype="float")
ds = data[:,0]
fc = data[:,1]

# In[3]:

# データの補間
f = interpolate.interp1d(ds, fc, kind='cubic')
rds = np.linspace(np.min(ds), np.max(ds), int(np.max(ds)-np.min(ds)))
rfc = f(rds)

# In[4]:

# FFT
sps = (np.max(ds)-np.min(ds))/(np.max(ds)-np.min(ds))
x = np.arange(0, len(rfc))/sps
spect = fftpack.fft(rfc)
amp = np.abs(spect) / len(rfc) / 2
phase = np.angle(spect)
freq = np.linspace(0, sps, len(rfc))

# In[8]:

# グラフ描画
plt.rcParams['font.size'] = 12
plt.rcParams['font.family'] = 'Sans'
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
ax1.yaxis.set_ticks_position('both')
ax1.xaxis.set_ticks_position('both')
ax2 = fig.add_subplot(212)
ax2.yaxis.set_ticks_position('both')
ax2.xaxis.set_ticks_position('both')
ax1.set_xlabel('Date [days]')
ax1.set_ylabel('Fuel consumption [km/L]')
ax2.set_xlabel('Period [days]')
ax2.set_ylabel('Fuel consumption [km/L]')
ax2.set_xticks(np.arange(5, 370, 4))
ax2.set_xlim(5, 370)
ax2.set_xscale('linear')
ax1.plot(x, rfc, label='Time waveform', lw=1, color='blue')
t = 1/freq[1:]　　　# 周波数を周期へ変換
ax2.plot(t, amp[1:], label='Amplitude', lw=0, marker=".", color='blue')
plt.show()
plt.close()

# In[ ]: