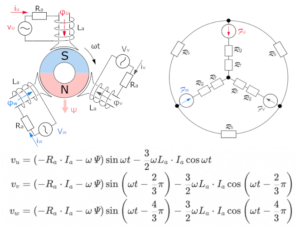
ブラシレスモータの電圧方程式

概要

3相ブラシレスモータの電圧方程式をモデルから導出する。d-q変換は使用しないで解く。モデルの構成は3相のコイルからなるステータと、2極の磁石からなるロータとする。3相の電圧と電流、2極の磁石の磁束から電圧方程式を求める。電気回路と磁気回路を各々定義してから数式を立てる。

Motor model of 3 phase PMSM

• Electric

  

• Magnetic
  

ロータの磁石からの磁束

ロータの磁石から発生し、U相V相W相の各コイルに鎖交する磁束を考える。
V相はU相に対し空間的に位相が\huge{\frac{2}{3}\pi} rad遅れており、W相はU相に対し空間的に位相が\huge{\frac{4}{3}\pi} rad遅れているので次式で表される。

\begin{aligned}
\psi_u &= \varPsi\cos\omega t \\
\psi_v &= \varPsi\cos\left( \omega t-\frac{2}{3}\pi \right) \\
\psi_w &= \varPsi\cos\left( \omega t-\frac{4}{3}\pi  \right) \\
\end{aligned}

ステータのコイルから発生する磁束

U相V相W相の各コイルに電流を流すことで発生する磁束はそれぞれ

\begin{aligned}
\phi_{uu} &=L_a\cdot i_u \\
\phi_{vv} &=L_a\cdot i_v \\
\phi_{ww} &=L_a\cdot i_w
\end{aligned}

U相コイルに電流を流すことで発生する磁束がV相コイルと鎖交する磁束を\huge{\phi_{uv}}、W相コイルと鎖交する磁束を\huge{\phi_{uw}}とすると

\begin{aligned}
\phi_{uv} &=-\frac{1}{2}L_a\cdot i_u \\
\phi_{uw} &=-\frac{1}{2}L_a\cdot i_u \\
\end{aligned}

V相コイルに電流を流すことで発生する磁束がW相コイルと鎖交する磁束を\huge{\phi_{vw}}、U相コイルと鎖交する磁束を\huge{\phi_{vu}}とすると

\begin{aligned}
\phi_{vw} &=-\frac{1}{2}L_a\cdot i_v \\
\phi_{vu} &=-\frac{1}{2}L_a\cdot i_v \\
\end{aligned}

W相コイルに電流を流すことで発生する磁束がU相コイルと鎖交する磁束を\huge{\phi_{wu}}、V相コイルと鎖交する磁束を\huge{\phi_{wv}}とすると

\begin{aligned}
\phi_{wu} &=-\frac{1}{2}L_a\cdot i_w \\
\phi_{wv} &=-\frac{1}{2}L_a\cdot i_w \\
\end{aligned}

ステータコイルに流す電流

ここでロータ磁束がU相コイルの鎖交磁束\huge{\psi_u}に対し時間的に\huge{\frac{\pi}{2}} rad進めた位相で電流をU相コイルへ流すことを考える。
同様にV相コイルの鎖交磁束\huge{\psi_v}に対し時間的に\huge{\frac{\pi}{2}} rad進めた位相で電流をV相コイルへ流し、
W相コイルの鎖交磁束\huge{\psi_w}に対し時間的に\huge{\frac{\pi}{2}} rad進めた位相で電流をW相コイルへ流す。

いわゆる弱め界磁がない状態である。(Id=0A)

\begin{aligned}
i_u &=I_a\cos\left(\omega t+\frac{1}{2}\pi \right) \\
&=-I_a\sin \omega t \\

i_v &=I_a\cos\left( \omega t-\frac{2}{3}\pi+\frac{1}{2}\pi \right) \\
&=-I_a\sin\left( \omega t-\frac{2}{3}\pi \right) \\

i_w &=I_a\cos\left( \omega t-\frac{4}{3}\pi+\frac{1}{2}\pi \right) \\
&=-I_a\sin\left( \omega t-\frac{2}{3}\pi  \right) \\
\end{aligned}

コイル電圧

コイル電圧はコイル抵抗の電圧降下と鎖交磁束の時間微分で得られる起電力の総和と等しくなることから次の式となる。

\begin{aligned}
v_u &=R_a\cdot i_u+\frac{d\psi_u}{dt}+\frac{d\phi_{uu}}{dt}+\frac{d\phi_{vu}}{dt}+\frac{d\phi_{wu}}{dt} \\
v_v &=R_a\cdot i_v+\frac{d\psi_v}{dt}+\frac{d\phi_{vv}}{dt}+\frac{d\phi_{wv}}{dt}+\frac{d\phi_{uv}}{dt} \\
v_w &=R_a\cdot i_w+\frac{d\psi_w}{dt}+\frac{d\phi_{ww}}{dt}+\frac{d\phi_{uw}}{dt}+\frac{d\phi_{vw}}{dt} \\
\end{aligned}

各項目を計算する。

電圧Vuの計算

\begin{aligned}

R_a\cdot i_u &=-R_a\cdot I_a\sin\omega t \\

\frac{d\psi_u}{dt} &=\frac{d}{dt}\left( \varPsi\cos\omega t \right) \\
&=-\omega\varPsi\sin\omega t \\

\frac{d\phi_{uu}}{dt} &=\frac{dL_a\cdot i_u}{dt} \\
&=L_a\frac{d}{dt}\left( -I_a\sin\omega t \right) \\
&=-\omega L_a\cdot I_a\cos\omega t \\

\frac{d\phi_{vu}}{dt} &=\frac{d}{dt}\left( -\frac{1}{2}L_a\cdot i_v \right) \\
&=-\frac{1}{2}L_a\frac{d}{dt}\left\{- I_a\sin\left(\omega t-\frac{2}{3}\pi \right)\right\} \\
&=\frac{1}{2}\omega L_a\cdot I_a\cos \left( \omega t-\frac{2}{3}\pi \right) \\
&= \frac{1}{2}\omega L_a\cdot I_a\left( \cos\omega t\cos\frac{2}{3}\pi +\sin\omega t\sin\frac{2}{3}\pi \right) \\
&= \frac{1}{2}\omega L_a\cdot I_a\left( -\frac{1}{2}\cos\omega t +\frac{\sqrt{3}}{2}\sin\omega t \right) \\

\frac{d\phi_{wu}}{dt} &=\frac{d}{dt}\left( -\frac{1}{2}L_a\cdot i_w \right) \\
&=-\frac{1}{2}L_a\frac{d}{dt}\left\{- I_a\sin\left(\omega t-\frac{4}{3}\pi \right)\right\} \\
&=\frac{1}{2}\omega L_a\cdot I_a\cos \left( \omega t-\frac{4}{3}\pi \right) \\
&=\frac{1}{2}\omega L_a\cdot I_a\left( \cos\omega t\cos\frac{4}{3}\pi+\sin\omega t\sin\frac{4}{3}\pi \right) \\
&=\frac{1}{2}\omega L_a\cdot I_a\left( -\frac{1}{2}\cos\omega t-\frac{\sqrt{3}}{2}\sin\omega t \right) \\

\end{aligned} \\

\begin{aligned}

\frac{d\phi_{uu}}{dt}+\frac{d\phi_{vu}}{dt}+\frac{d\phi_{wu}}{dt} &=\omega L_a\cdot I_a\left( -\cos\omega t-\frac{1}{4}\cos \omega t+\frac{\sqrt{3}}{4}\sin\omega t-\frac{1}{4}\cos\omega t-\frac{\sqrt{3}}{4}\sin\omega t \right) \\
&=-\frac{3}{2}\omega L_a\cdot I_a\cos\omega t \\

\end{aligned}

以上より

\begin{aligned}
v_u&=-R_a\cdot I_a\sin\omega t-\omega\varPsi\sin\omega t-\frac{3}{2}\omega L_a\cdot I_a\cos\omega t \\
&=\left( -R_a\cdot I_a-\omega\varPsi \right) \sin\omega t-\frac{3}{2}\omega L_a\cdot I_a\cos\omega t
\end{aligned}

電圧Vvの計算

\begin{aligned}

R_a\cdot i_v &=-R_a\cdot I_a\sin\left( \omega t-\frac{2}{3}\pi \right) \\

\frac{d\psi_v}{dt} &=\frac{d}{dt}\left\{ \varPsi\cos\left( \omega t-\frac{2}{3}\pi \right) \right\} \\
&=-\omega\varPsi\sin\left( \omega t-\frac{2}{3}\pi \right) \\

\frac{d\phi_{vv}}{dt} &=\frac{dL_a\cdot i_v}{dt} \\
&=L_a\frac{d}{dt}\left\{ -I_a\sin\left(\omega t-\frac{2}{3}\pi \right) \right\} \\
&=-\omega L_a\cdot I_a\cos\left(\omega t-\frac{2}{3}\pi \right) \\
&=-\omega L_a\cdot I_a\left(\cos\omega t\cos\frac{2}{3}\pi+\sin\omega t\sin\frac{2}{3}\pi \right) \\
&=-\omega L_a\cdot I_a\left(-\frac{1}{2}\cos\omega t+\frac{\sqrt{3}}{2}\sin\omega t \right) \\

\frac{d\phi_{wv}}{dt} &=\frac{d}{dt}\left( -\frac{1}{2}L_a\cdot i_w \right) \\
&=-\frac{1}{2}L_a\frac{d}{dt}\left\{- I_a\sin\left(\omega t-\frac{4}{3}\pi \right)\right\} \\
&=\frac{1}{2}\omega L_a\cdot I_a\cos \left( \omega t-\frac{4}{3}\pi \right) \\
&= \frac{1}{2}\omega L_a\cdot I_a\left( \cos\omega t\cos\frac{4}{3}\pi +\sin\omega t\sin\frac{4}{3}\pi \right) \\
&= \frac{1}{2}\omega L_a\cdot I_a\left( -\frac{1}{2}\cos\omega t -\frac{\sqrt{3}}{2}\sin\omega t \right) \\

\frac{d\phi_{uv}}{dt} &=\frac{d}{dt}\left( -\frac{1}{2}L_a\cdot i_u \right) \\
&=-\frac{1}{2}L_a\frac{d}{dt}\left(- I_a\sin\omega t\right) \\
&=\frac{1}{2}\omega L_a\cdot I_a\cos\omega t \\

\end{aligned} \\

\begin{aligned}

\frac{d\phi_{vv}}{dt}+\frac{d\phi_{wv}}{dt}+\frac{d\phi_{uv}}{dt} &=\omega L_a\cdot I_a\left( \frac{1}{2}\cos\omega t-\frac{\sqrt{3}}{2}\sin\omega t -\frac{1}{4}\cos\omega t -\frac{\sqrt{3}}{4}\sin\omega t + \frac{1}{2}\cos\omega t  \right) \\
&=\omega L_a\cdot I_a\left( \frac{3}{4}\cos\omega t -\frac{3\sqrt{3}}{4}\sin\omega t \right) \\
&=-\frac{3}{2}\omega L_a\cdot I_a\left( -\frac{1}{2}\cos\omega t +\frac{\sqrt{3}}{2}\sin\omega t \right) \\
&=-\frac{3}{2}\omega L_a\cdot I_a\left( \cos\omega t\cos\frac{2}{3}\pi +\sin\omega t\sin\frac{2}{3}\pi \right) \\
&=-\frac{3}{2}\omega L_a\cdot I_a  \cos\left(\omega t -\frac{2}{3}\pi \right) \\

\end{aligned}

以上より

\begin{aligned}
v_v&=-R_a\cdot I_a\sin\left( \omega t-\frac{2}{3}\pi \right)-\omega\varPsi\sin\left(\omega t -\frac{2}{3}\pi \right)-\frac{3}{2}\omega L_a\cdot I_a\cos\left(\omega t -\frac{2}{3}\pi \right) \\
&=\left( -R_a\cdot I_a-\omega\varPsi \right) \sin\left(\omega t -\frac{2}{3}\pi \right)-\frac{3}{2}\omega L_a\cdot I_a\cos\left(\omega t -\frac{2}{3}\pi \right)
\end{aligned}

電圧Vwの計算

\begin{aligned}

R_a\cdot i_w &=-R_a\cdot I_a\sin\left( \omega t-\frac{4}{3}\pi \right) \\

\frac{d\psi_w}{dt} &=\frac{d}{dt}\left\{ \varPsi\cos\left( \omega t-\frac{4}{3}\pi \right) \right\} \\
&=-\omega\varPsi\sin\left( \omega t-\frac{4}{3}\pi \right) \\

\frac{d\phi_{ww}}{dt} &=\frac{dL_a\cdot i_w}{dt} \\
&=L_a\frac{d}{dt}\left\{ -I_a\sin\left(\omega t-\frac{4}{3}\pi \right) \right\} \\
&=-\omega L_a\cdot I_a\cos\left(\omega t-\frac{4}{3}\pi \right) \\
&=-\omega L_a\cdot I_a\left(\cos\omega t\cos\frac{4}{3}\pi+\sin\omega t\sin\frac{4}{3}\pi \right) \\
&=-\omega L_a\cdot I_a\left(-\frac{1}{2}\cos\omega t-\frac{\sqrt{3}}{2}\sin\omega t \right) \\

\frac{d\phi_{uw}}{dt} &=\frac{d}{dt}\left( -\frac{1}{2}L_a\cdot i_u \right) \\
&=-\frac{1}{2}L_a\frac{d}{dt}\left( - I_a\sin\omega t \right) \\
&=\frac{1}{2}\omega L_a\cdot I_a\cos \omega t \\

\frac{d\phi_{vw}}{dt} &=\frac{d}{dt}\left( -\frac{1}{2}L_a\cdot i_v \right) \\
&=-\frac{1}{2}L_a\frac{d}{dt}\left\{ - I_a\sin\left( \omega t -\frac{2}{3}\pi \right) \right\} \\
&=\frac{1}{2}\omega L_a\cdot I_a\cos\left( \omega t -\frac{2}{3}\pi \right) \\
&=\frac{1}{2}\omega L_a\cdot I_a\left(\cos\omega t\cos\frac{2}{3}\pi+\sin\omega t\sin\frac{2}{3}\pi \right) \\
&=\frac{1}{2}\omega L_a\cdot I_a\left(-\frac{1}{2}\cos\omega t+\frac{\sqrt{3}}{2}\sin\omega t \right) \\

\end{aligned} \\

\begin{aligned}

\frac{d\phi_{ww}}{dt}+\frac{d\phi_{uw}}{dt}+\frac{d\phi_{vw}}{dt} &=\omega L_a\cdot I_a\left( \frac{1}{2}\cos\omega t+\frac{\sqrt{3}}{2}\sin\omega t +\frac{1}{2}\cos\omega t -\frac{1}{4}\cos\omega t +\frac{\sqrt{3}}{4}\sin\omega t \right) \\
&=\omega L_a\cdot I_a\left( \frac{3}{4}\cos\omega t +\frac{3\sqrt{3}}{4}\sin\omega t \right) \\
&=-\frac{3}{2}\omega L_a\cdot I_a\left( -\frac{1}{2}\cos\omega t -\frac{\sqrt{3}}{2}\sin\omega t \right) \\
&=-\frac{3}{2}\omega L_a\cdot I_a\left( \cos\omega t\cos\frac{4}{3}\pi +\sin\omega t \sin\frac{4}{3}\pi \right) \\
&=-\frac{3}{2}\omega L_a\cdot I_a  \cos\left(\omega t -\frac{4}{3}\pi \right) \\

\end{aligned}

以上より

\begin{aligned}
v_w&=-R_a\cdot I_a\sin\left( \omega t-\frac{4}{3}\pi \right)-\omega\varPsi\sin\left(\omega t -\frac{4}{3}\pi \right)-\frac{3}{2}\omega L_a\cdot I_a\cos\left(\omega t -\frac{4}{3}\pi \right) \\
&=\left( -R_a\cdot I_a-\omega\varPsi \right) \sin\left(\omega t -\frac{4}{3}\pi \right)-\frac{3}{2}\omega L_a\cdot I_a\cos\left(\omega t -\frac{4}{3}\pi \right)
\end{aligned}

電圧方程式

まとめると電圧方程式は下記となる。

\begin{aligned}
v_u&=\left( -R_a\cdot I_a-\omega\varPsi \right) \sin\omega t-\frac{3}{2}\omega L_a\cdot I_a\cos\omega t \\
v_v&=\left( -R_a\cdot I_a-\omega\varPsi \right) \sin\left(\omega t -\frac{2}{3}\pi \right)-\frac{3}{2}\omega L_a\cdot I_a\cos\left(\omega t -\frac{2}{3}\pi \right) \\
v_w&=\left( -R_a\cdot I_a-\omega\varPsi \right) \sin\left(\omega t -\frac{4}{3}\pi \right)-\frac{3}{2}\omega L_a\cdot I_a\cos\left(\omega t -\frac{4}{3}\pi \right) \\
\end{aligned}