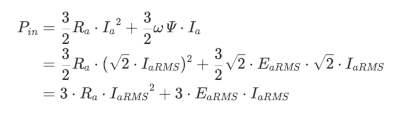
概要
ブラシレスモータの電圧方程式から入力電力を計算し、モータ出力について考える。dーq変換は使用しない。
電圧方程式
電圧方程式は下記であるので、
\begin{aligned}
v_u&=\left( -R_a\cdot I_a-\omega\varPsi \right) \sin\omega t-\frac{3}{2}\omega L_a\cdot I_a\cos\omega t \\
v_v&=\left( -R_a\cdot I_a-\omega\varPsi \right) \sin\left(\omega t -\frac{2}{3}\pi \right)-\frac{3}{2}\omega L_a\cdot I_a\cos\left(\omega t -\frac{2}{3}\pi \right) \\
v_w&=\left( -R_a\cdot I_a-\omega\varPsi \right) \sin\left(\omega t -\frac{4}{3}\pi \right)-\frac{3}{2}\omega L_a\cdot I_a\cos\left(\omega t -\frac{4}{3}\pi \right) \\
\end{aligned}モータの入力電力
3相各々の電圧と電流を積算しモータの入力電力を計算する。
\begin{aligned}
P_{in} &=v_u\cdot i_u+v_v\cdot i_v+v_w\cdot i_w
\end{aligned}U相の電力
\begin{aligned}
v_u\cdot i_u &=\left\{ \left( -R_a\cdot I_a-\omega\varPsi \right) \sin\omega t-\frac{3}{2}\omega L_a\cdot I_a\cos\omega t \right\}
(-I_a\sin \omega t) \\
&=\left( R_a\cdot I_a^2+\omega\varPsi\cdot I_a\right) \sin^2\omega t+\frac{3}{2}\omega L_a\cdot I_a^2\sin\omega t\cos\omega t \\
&=\left( R_a\cdot I_a^2+\omega\varPsi\cdot I_a \right) \frac{1-\cos2\omega t}{2}+\frac{3}{2}\omega L_a\cdot I_a^2\frac{\sin2\omega t}{2} \\
&=\left( \frac{R_a\cdot I_a^2}{2}+\frac{\omega\varPsi\cdot I_a}{2} \right) \left( 1-\cos2\omega t \right) +\frac{3}{2}\cdot\frac{\omega L_a\cdot I_a^2}{2}\sin2\omega t \\
\end{aligned}V相の電力
\begin{aligned}
v_v\cdot i_v &=\left\{ \left( -R_a\cdot I_a-\omega\varPsi \right) \sin\left( \omega t-\frac{2}{3}\pi \right)-\frac{3}{2}\omega L_a\cdot I_a\cos\left( \omega t-\frac{2}{3}\pi \right) \right\}
\left\{ -I_a\sin\left( \omega t-\frac{2}{3}\pi \right)) \right\} \\
&=\left( R_a\cdot I_a^2+\omega\varPsi\cdot I_a \right) \sin^2\left( \omega t-\frac{2}{3}\pi \right)+\frac{3}{2}\omega L_a\cdot I_a^2\sin\left( \omega t-\frac{2}{3}\pi \right)\cos\left( \omega t-\frac{2}{3}\pi \right) \\
&=\left( R_a\cdot I_a^2+\omega\varPsi\cdot I_a \right) \frac{1-\cos2\left( \omega t-\frac{2}{3}\pi \right)}{2}+\frac{3}{2}\omega L_a\cdot I_a^2\frac{\sin2\left( \omega t-\frac{2}{3}\pi \right)}{2} \\
&=\left( \frac{R_a\cdot I_a^2}{2}+\frac{\omega\varPsi\cdot I_a}{2} \right) \left\{ 1-\cos\left( 2\omega t-\frac{4}{3}\pi \right) \right\}
+\frac{3}{2}\cdot \frac{\omega L_a\cdot I_a^2}{2}\sin\left( 2\omega t-\frac{4}{3}\pi \right) \\
&=\left( \frac{R_a\cdot I_a^2}{2}+\frac{\omega\varPsi\cdot I_a}{2} \right) \left( 1-\cos 2\omega t\cos\frac{4}{3}\pi-\sin 2\omega t\sin\frac{4}{3}\pi \right)
+\frac{3}{2}\cdot \frac{\omega L_a\cdot I_a^2}{2}\left(\sin 2\omega t\cos\frac{4}{3}\pi-\cos 2\omega t\sin\frac{4}{3}\pi \right) \\
&=\left( \frac{R_a\cdot I_a^2}{2}+\frac{\omega\varPsi\cdot I_a}{2} \right) \left( 1+\frac{1}{2}\cos 2\omega t+\frac{\sqrt{3}}{2}\sin 2\omega t \right)
+\frac{3}{2}\cdot \frac{\omega L_a\cdot I_a^2}{2}\left(-\frac{1}{2}\sin 2\omega t+\frac{\sqrt{3}}{2}\cos 2\omega t \right) \\
\end{aligned}W相の電力
\begin{aligned}
v_w\cdot i_w &=\left\{ \left( -R_a\cdot I_a-\omega\varPsi \right) \sin\left( \omega t-\frac{4}{3}\pi \right)-\frac{3}{2}\omega L_a\cdot I_a\cos\left( \omega t-\frac{4}{3}\pi \right) \right\}
\left\{ -I_a\sin\left( \omega t-\frac{4}{3}\pi \right)) \right\} \\
&=\left( R_a\cdot I_a^2+\omega\varPsi\cdot I_a \right) \sin^2\left( \omega t-\frac{4}{3}\pi \right)+\frac{3}{2}\omega L_a\cdot I_a^2\sin\left( \omega t-\frac{4}{3}\pi \right)\cos\left( \omega t-\frac{4}{3}\pi \right) \\
&=\left( R_a\cdot I_a^2+\omega\varPsi\cdot I_a \right) \frac{1-\cos2\left( \omega t-\frac{4}{3}\pi \right)}{2}+\frac{3}{2}\omega L_a\cdot I_a^2\frac{\sin2\left( \omega t-\frac{4}{3}\pi \right)}{2} \\
&=\left( \frac{R_a\cdot I_a^2}{2}+\frac{\omega\varPsi\cdot I_a}{2} \right)\left\{ 1-\cos\left( 2\omega t-\frac{8}{3}\pi \right) \right\} +\frac{3}{2}\omega L_a\cdot \frac{I_a^2}{2} \sin\left( 2\omega t-\frac{8}{3}\pi \right) \\
&=\left( \frac{R_a\cdot I_a^2}{2}+\frac{\omega\varPsi\cdot I_a}{2} \right)\left( 1-\cos2\omega t\cos\frac{8}{3}\pi-\sin2\omega t\sin\frac{8}{3}\pi \right) + \frac{3}{2}\omega L_a\cdot \frac{I_a^2}{2} \left( \sin 2\omega t \cos\frac{8}{3}\pi - \cos\omega t\sin\frac{8}{3}\pi \right) \\
&=\left( \frac{R_a\cdot I_a^2}{2}+\frac{\omega\varPsi\cdot I_a}{2} \right)\left( 1+\frac{1}{2}\cos2\omega t - \frac{\sqrt{3}}{2}\sin2\omega t \right) + \frac{3}{2}\cdot\frac{\omega L_a\cdot I_a^2}{2} \left( -\frac{1}{2}\sin 2\omega t - \frac{\sqrt{3}}{2}\cos\omega t \right) \\
\end{aligned}以上よりモータの入力電力は
\begin{aligned}
P_{in} &=v_u\cdot i_u+v_v\cdot i_v+v_w\cdot i_w \\
&=\left( \frac{R_a\cdot I_a^2}{2}+\frac{\omega\varPsi\cdot I_a}{2} \right) \left( 1-\cos2\omega t \right) +\frac{3}{2}\cdot\frac{\omega L_a\cdot I_a^2}{2}\sin2\omega t \\
&+\left( \frac{R_a\cdot I_a^2}{2}+\frac{\omega\varPsi\cdot I_a}{2} \right) \left( 1+\frac{1}{2}\cos 2\omega t+\frac{\sqrt{3}}{2}\sin 2\omega t \right)
+\frac{3}{2}\cdot \frac{\omega L_a\cdot I_a^2}{2}\left(-\frac{1}{2}\sin 2\omega t+\frac{\sqrt{3}}{2}\cos 2\omega t \right) \\
&+\left( \frac{R_a\cdot I_a^2}{2}+\frac{\omega\varPsi\cdot I_a}{2} \right)\left( 1+\frac{1}{2}\cos2\omega t - \frac{\sqrt{3}}{2}\sin2\omega t \right) + \frac{3}{2}\cdot\frac{\omega L_a\cdot I_a^2}{2} \left( -\frac{1}{2}\sin 2\omega t - \frac{\sqrt{3}}{2}\cos\omega t \right) \\
&=\left( \frac{R_a\cdot I_a^2}{2}+\frac{\omega\varPsi\cdot I_a}{2} \right) (3) +\frac{3}{2}\cdot\frac{\omega L_a\cdot I_a^2}{2}(0) \\
&=\frac{3}{2}R_a\cdot I_a^2+\frac{3}{2}\omega\varPsi\cdot I_a \\
\end{aligned}第1項はモータの銅損を表し第2項はモータの速度起電力を表す。速度起電力が機械出力へ変換されるので
\begin{aligned}
P_{in}&=P_{loss}+P_m \\
P_{loss}&=\frac{3}{2}R_a\cdot I_a^2 \\
P_m&=\frac{3}{2}\omega\varPsi\cdot I_a
\end{aligned}また、機械出力は回転角速度とトルクの積であるので
\begin{aligned}
P_m &=\omega \cdot \tau \\
\tau &=\frac{3}{2}\varPsi\cdot I_a
\end{aligned}実効値表現
入力電力を実効値で表現すると
\begin{aligned}
I_a &=\sqrt2\cdot I_{aRMS} \\
E_a &=\omega \varPsi \\
&=\sqrt2\cdot E_{aRMS} \\
\end{aligned}より
\begin{aligned}
P_{in}&=\frac{3}{2}R_a\cdot {I_a}^2+\frac{3}{2}\omega\varPsi\cdot I_a \\
&=\frac{3}{2}R_a\cdot (\sqrt2\cdot I_{aRMS})^2+\frac{3}{2}\sqrt2\cdot E_{aRMS}\cdot \sqrt2\cdot I_{aRMS} \\
&=3\cdot R_a\cdot {I_{aRMS}}^2+3\cdot E_{aRMS}\cdot I_{aRMS} \\
\end{aligned}